三、二室模型一级消除动力学
多室模型和前面讨论的单室模型不同,此时存在着由包括血液在内的中央室向周边室分布达到平衡的过程,影响血药浓度的因素更为复杂,下面以单剂静脉注射为例,简介有关药动学知识。
(一)模式图和药-时关系
静脉注射时,不存在吸收过程,中央室中的药量或血药浓度受中央室与周边室间双向分布,以及自中央室消除的影响。其模式如图9-9所示。
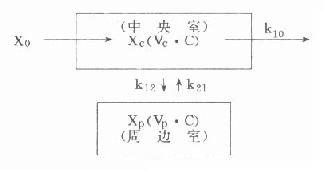
xc中央室药量
xp周边室药量
vc中央室分布容积
vp周边室分布容积
k10中央室向周边室转运速率常数
k21周边室向中央室转运速率常数
图9-9 二室分布静脉注射模式图
中央室药量变化的速率微分方程为:
dkc/dt=k21·xp-k21·xc-k10·xc
对上式积分并引入中央室分布容积Vc,可得中央室(血)药物浓度随时间变化的基本表达式:
C=A·e+B·e-βt式(25)
式中α为分布速率常数,β为消除速率常数,A、B为经验常数。四者都是由模式参数k10、k12、k21组成的混杂参数(hybridparameters)。存在:
α·β=k21·k10α+β=k10+k12+k21
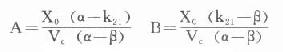
(二)药动学参数计算
二室模型静脉注射药动学参数的求算,类似于单室模型血管外用药,仍采用残数法。即因为α>β,当t充分大时,A·e-αt→0,则式(25)变为
C=Be-βt
此即消除相药-时关系表达式。按前述方法可求得B、β和消除半寿期t1/2β。将式(25)移项可得:
C-B·e-αt=A·e-αt
令Cr=C-B·e-βt,Cr即为消除相以前某时点实测血药浓度减去消除相该点外推浓度的残数。代入上式可得分布相药-时关系表达式
Cr=A·e-αt
同样可求得A、α和分布半寿期t1/2α(图9-10)。
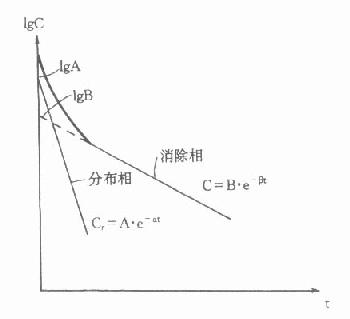
图9-10 二室模型静脉注射血药浓度-时间关系示意图
再根据下列公式,可求得各有关药动学参数。
中央室表观分布容积:Vc=X0/(A+B)
周边室向中央室的转运速率常数:
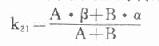
自中央室消除的速率常数:
k10=α·β/k21
中央室向周边室转运的速率常数:
k12=(α+β)-(k10+k21)
曲线下面积:AUC0→∞=A/α+B/β(积分外推法)
周边室表观分布容积:Vp=Vc·k12/k21
总表观分布容积:
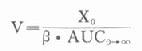
稳态表观分布容积:Vss=Vc+Vp
消除率:Cl=k10·Vc=β·V
血管外用药时,由于存在吸收因素,求算药动学参数的基本方法仍为残数法,但此时需进行两次残数处理。有关二室模型血管外用药及二室以上多室模型的药动学,在TDM的实际工作中很少应用,可参阅有关药动学专著。
| 上一页:二、单室模型一级消除动力学 |
| 当前页:三、二室模型一级消除动力学 |
| 下一页:四、非线性动力学 |